 The development of a new medicine takes typically over 12 years or even longer [1]. When not taking into account the clinical trial or other stages of drug discovery, the stage of designing molecules for pharmaceuticals itself is a time-consuming process and prone to error. To do molecule design, one needs to search through the vast chemical space that includes all possible compounds to find the lead molecule. The chemical space of potential drugs contains more than \(10^{60}\) molecules [2]. Navigating in such space to find the molecules with the desired properties is extremely hard as the chemical space is discrete and small changes in a molecule can change radically its properties.
The development of a new medicine takes typically over 12 years or even longer [1]. When not taking into account the clinical trial or other stages of drug discovery, the stage of designing molecules for pharmaceuticals itself is a time-consuming process and prone to error. To do molecule design, one needs to search through the vast chemical space that includes all possible compounds to find the lead molecule. The chemical space of potential drugs contains more than \(10^{60}\) molecules [2]. Navigating in such space to find the molecules with the desired properties is extremely hard as the chemical space is discrete and small changes in a molecule can change radically its properties.
Instead of treating molecule design as a search algorithm in a discrete space, we can treat it as a generation problem, where the machine learning model generates candidate molecules exhibiting requested properties. Such candidate molecules generated by the model will have a high probability of success in the life experiment in the lab. As a result, this automated molecule design process will drastically reduce the cost of drug design and lead to a huge impact on drug discovery as well as material design-related applications. Though machine learning approaches have shown great success in estimating properties of small molecules, the inverse problem of generating molecules with desired properties remains challenging. This difficulty is in part because of the discrete nature of molecule space and the fact that for a given property, we have a set of molecules that are structurally very diverse.
Molecule discovery tasks come in two flavors. Global optimization seeks to find molecules that have a particular target property. Local optimization starts from some initial molecule and searches for molecules that have the desired property while not straying too far from the prototype. From existing generative models, if designed properly, the autoregressive model can be a good candidate for global optimization while the latent variable model can do both global and local optimization. Most of the existing works handle this task in two-step optimization fashion [5][6][7], where they either use a genetic algorithm or other models to generate a large number of candidates then do filtering, or they apply VAE models to map the discrete molecules into continuous latent space and then do optimization in that space. Here we propose a one-step approach that can do both global and local optimization of the molecule.
Latent variable model for conditional molecule generation and style transfer
Assume that molecules are generated by a set of latent factors \(\mathbf z\) and a set of observed property \(\mathbf y\):
With this assumption, we can model the conditional distribution with a latent variable \(\mathbf z\) such that:
So once we learn the generative distribution \(P_{\theta}(\mathbf x | \mathbf y, \mathbf z)\), we can generate new molecules with a desired property \(\mathbf y'\) in two ways:

To learn \(P_{\theta}(\mathbf x | \mathbf y, \mathbf z)\), we follow varional auto encoder setting where the generative model is coupled with a encoder \(q_{\phi}(\mathbf z| \mathbf x)\), and learned through maximizing the lower bound of \(\log p_{\theta}(\mathbf x, \mathbf y)\) which is normally referred to as ELBO (evidance lower bound).

However, as the objective only considers reconstruction error, and given that we have vanilla VAE models with the generative model \(P_{\theta}(\mathbf x | \mathbf z)\), which only takes \(\mathbf z\) as input, is capable of reconstructing back the molecule, there is a risk of directly applying above model for conditional generation. The generative model could ignores \(\mathbf y\) and only reconstruct from \(\mathbf z\), this will lead to a generative model that does ignores the conditioning factor \(\mathbf y\) and only generates from latent factor \(\mathbf z\). Therefore we add a constrain to the above objective to force it take into accoun the \(\mathbf y\) given to the generative network:
Assume the we represent RDKit with an oracle function \( f\), what is the extra constrain does here is that it will force every generated molecule that is generated from by conditioning on the target \(\mathbf y\) to have a property close to \(\mathbf y\). The full model is explained in the following diagram:
With above soft constrain, we in fact, introduced a disentangling regularizer that encourages the latent factor \(\mathbf z\) and property \(\mathbf y\) to be disentangled, which means, the property information to generate molecules can only come from the \(\mathbf y\) that is given to the generative network, not from \(\mathbf z\), therefore, the encoder will learn to encode information into \(\mathbf z\) everything about that molecule but not the property information.
![]()
Dealing with non-differentiability
The regularizer we introduced in the constrained ELBO is non-differentiable both due to the non-differentiable function \( f\) and sampled molecule \(\hat{\mathbf x}\) which is discrete. To be able to use gradient-based optimization, we side-step the non-differentiability by using decoder output as a continuous representation of molecule and pre-training a property predictor \(f_{\omega}\) that approximate the RDKit value from continuous representation. Here is the full pipeline: 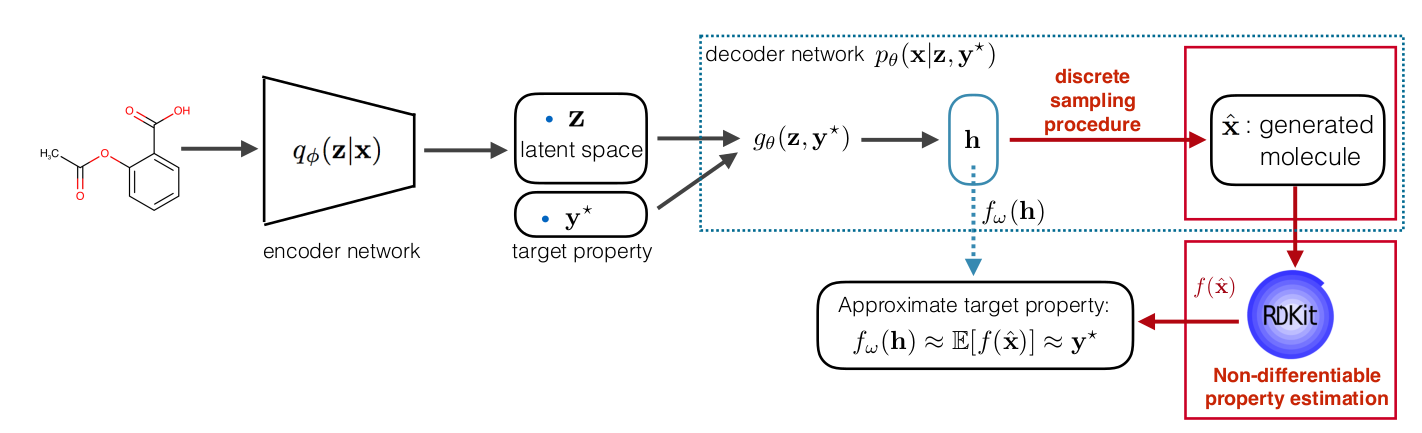
For more details please visit refer to the full paper [5]
Results
To show the effectiveness of the added constraint, we applied our model on two publically available datasets: QM9 and ZINC. We used the grammar-based[6] representation of molecules and chose logP as the conditioning property.
Before proceeding to conditional generation, we tested if the added regularizer will affect the generation performance or not, here in Table 1 you will see the generation results when compared to the baselines.
- Generation performance when compared to the baselines
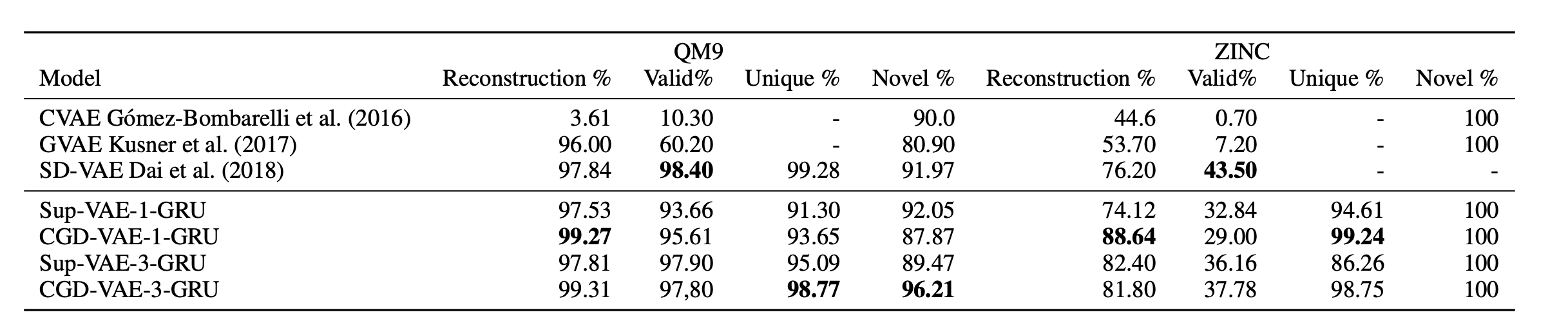
Table 1: Reconstruction performance and generation quality (Valid, Unique, Novel).
- condtional generation performance:
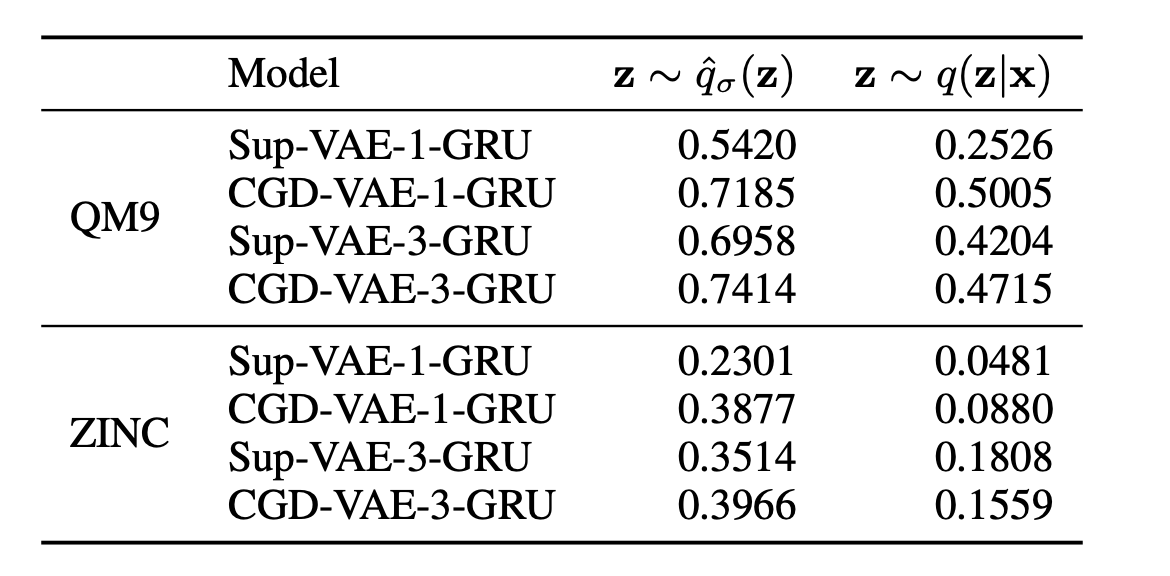
Table 2: Correlation between the desired input property and the obtained property.
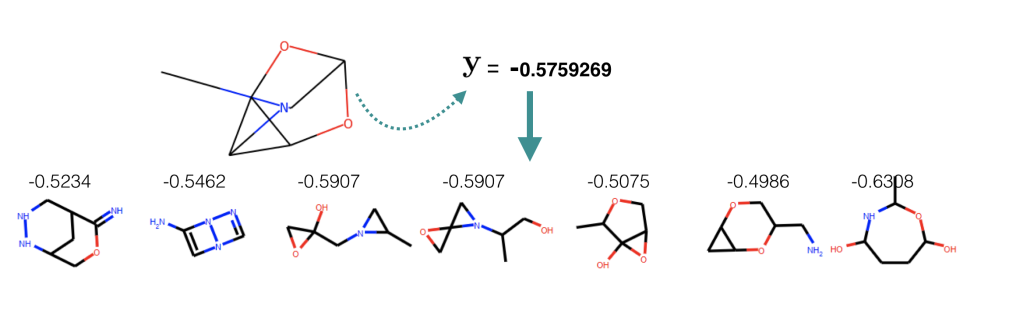
Further more, as a demo for conditional generation, we set logP: \( \mathbf y = −0.5759269 \) and sample molecules from \(P_{\theta}(\mathbf x | \mathbf y, \mathbf z)\) where \(\mathbf z\) is sampled from approximated aggregated posterior. Among 50 generation, seven of them have property that is whithin 15% range from the target.
Below is a style transfer demo for one molecule, where we try to generate a new molecule that is structurally similar to molecule A and has the property of molecule B. More precisely, we encode the molecule A to get latent factor \(\mathbf z\) and set the \(\mathbf y\) value to molecule B property, then sample from the generative model.
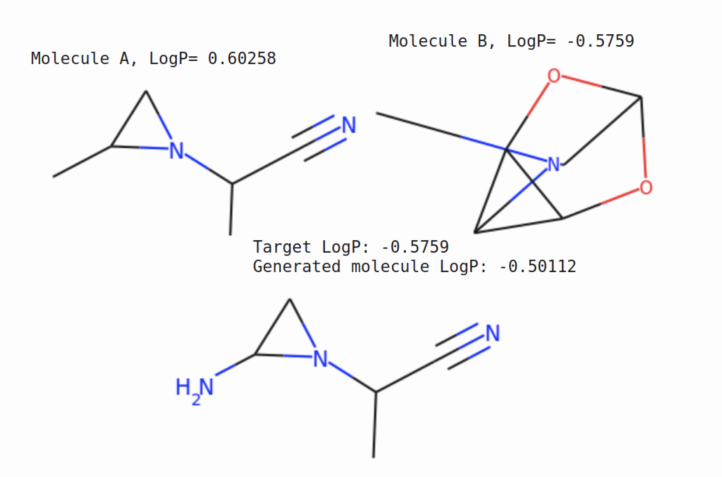
For more results, refer to the full paper
Sequence models for conditional molecule generation
Suppose we are given N training examples \({\mathbf x_i,\mathbf y_i }\), where \(\mathbf x_i\) represents a molecule and \(\mathbf y_i\) represents the corresponding property vector. If we use SMILES representation of the molecules, we could treat a molecule as a sequence of character \(\mathbf x_i = \mathbf x_{i12...T}\) with maximum length T. A very straight forward way would be using LSTM to model conditional distribution \(p_{\theta}(\mathbf x|\mathbf y)\) and learn it by maximizing the conditional log-likelihood objective. We modify an existing sequence generation model [3] that learns \(p_{\theta}(\mathbf x)\) to learn \(p_{\theta}(\mathbf x|\mathbf y)\):
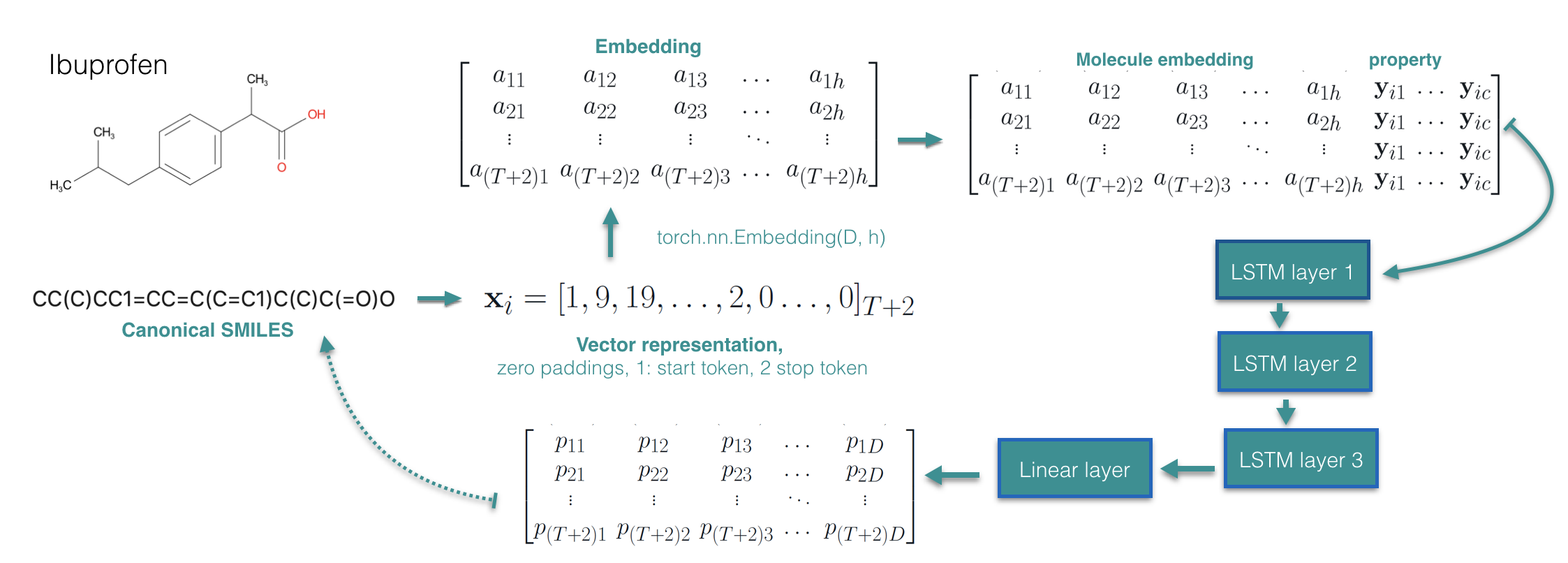
We applied the above model on Guacamol dataset [4] where we condition on nine properties including continuous and discrete values such as the number of rotatable bonds, aromatic rings, logP, QED-score, molecule weight as so on. For generation performance, we achieve 89.5 % validity, 99.9% unicity, and 99% novelty. Regarding the conditional generation performance, we measure the correlation coefficient between the conditioned value of the property and obtained molecules property, for all the nine properties, we achieve above near 0.99 except the QED score, see the figure below:

Correlation between the target property that is given to the LSTM model and property of the generated molecule
Conclusion
Machine learning models have huge potential in molecule design. Autoregressive models perform very well for the conditional generation of molecule, however, it can not do style transfer since it has no control over the structure of molecules it generates. While VAE models can do both conditional generation and style transfer, it's performance still need to be further enhanced.
Reference
[1] DiMasi, J. A., Feldman, L., Seckler, A., and Wilson, A. (2010). Trends in risks associated with new drug development: success rates for investigational drugs. Clinical Pharmacology & Therapeutics, 87(3):272–277. [2] DiMasi, J. A., Grabowski, H. G., and Hansen, R. W. (2016). Innovation inthe pharmaceutical industry: new estimates of r&d costs. Journal of health economics, 47:20–33. [3] Brown, N., Fiscato, M., Segler, M. H., and Vaucher, A. C. (2019). Guacamol: benchmarking models for de novo molecular design. Journal of chemical information and modeling, 59(3):1096–1108. [4] Mendez, D., Gaulton, A., Bento, A. P., Chambers, J., De Veij, M., Félix, E., Magariños, M. P., Mosquera, J. F., Mutowo, P., Nowotka, M., et al. (2018). Chembl: towards direct deposition of bioassay data. Nucleic acids research, 47(D1):D930–D940. [5] Go ́mez-Bombarelli, R., Duvenaud, D. K., Herna ́ndez-Lobato, J. M., Aguilera-Iparraguirre, J., Hirzel, T. D., Adams, R. P., and Aspuru-Guzik, A. (2016). Automatic chemical design using a data-driven continuous representation of molecules. CoRR, abs/1610.02415. [6] Kusner, M. J., Paige, B., and Herna ́ndez-Lobato, J. M. (2017). Grammar variational autoencoder. arXiv preprint arXiv:1703.01925. [7] Dai, H., Tian, Y., Dai, B., Skiena, S., and Song, L. (2018). Syntax-directed variational autoencoder for structured data. arXiv preprint arXiv:1802.08786.